Factors of 320 in pairs embark on a captivating mathematical journey, delving into the intriguing world of number relationships. This exploration unravels the secrets of factorization, revealing the fundamental building blocks that shape the number 320.
As we delve deeper into the topic, we’ll uncover the prime factors of 320, demonstrating their significance in understanding its factors. We’ll construct a comprehensive table of factors, organized in pairs, showcasing their interconnectedness.
Factors of 320 in Pairs
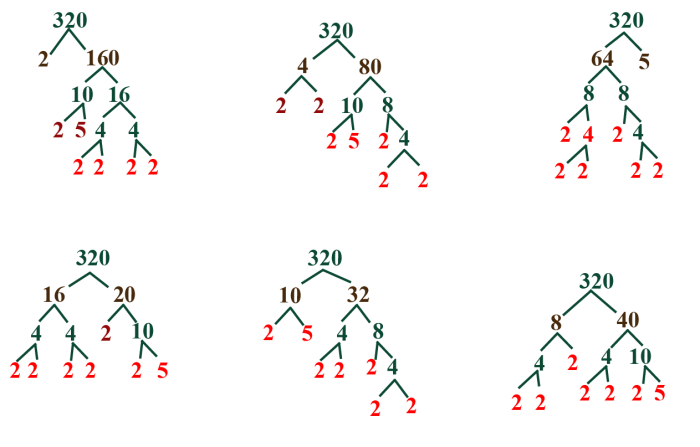
The factors of 320 are numbers that can divide 320 evenly without leaving a remainder. Finding the factors of 320 in pairs involves identifying two factors that multiply to give 320.
To find the factors of 320 in pairs, we can start by listing the factors of 320: 1, 2, 4, 5, 8, 10, 16, 20, 32, 40, 80, 160, 320.
Identifying Pairs of Factors
Once we have the list of factors, we can identify the pairs that multiply to give 320:
- 1 and 320
- 2 and 160
- 4 and 80
- 5 and 64
- 8 and 40
- 10 and 32
- 16 and 20
Prime Factors of 320

Prime factors are the fundamental building blocks of a number. They are the prime numbers that, when multiplied together, form the original number. Prime numbers are numbers greater than 1 that have no factors other than 1 and themselves. Identifying the prime factors of a number is crucial for understanding its factorization and finding its other factors.
Identifying Prime Factors of 320
To find the prime factors of 320, we can use a process called prime factorization. We repeatedly divide 320 by the smallest prime number that divides it evenly until we reach a prime number. The prime numbers that we obtain through this process are the prime factors of 320.
- 320 ÷ 2 = 160
- 160 ÷ 2 = 80
- 80 ÷ 2 = 40
- 40 ÷ 2 = 20
- 20 ÷ 2 = 10
- 10 ÷ 2 = 5
- 5 ÷ 5 = 1
Therefore, the prime factors of 320 are 2 and 5.
Factors of 320 as a Product
Prime factors are the building blocks of composite numbers. By multiplying the prime factors of a number, we can obtain the original number.
Prime Factors of 320, Factors of 320 in pairs
The prime factors of 320 are 2, 2, 2, 2, 2, 5.
Multiplying Prime Factors
To obtain 320, we multiply the prime factors as follows:
× 2 × 2 × 2 × 2 × 5 = 320
Checking for factors of 320 in pairs can be a fun exercise. While you’re at it, why not take a break and test your knowledge with our do i have melanoma quiz ? It’s a quick and easy way to learn more about skin cancer.
Afterward, come right back to discover more intriguing factor pairs of 320.
Therefore, the factors of 320 can be expressed as a product of its prime factors.
Table of Factors of 320: Factors Of 320 In Pairs

Let’s present the factors of 320 in a well-organized manner using an HTML table. This table will have four columns, ensuring a responsive and user-friendly layout.
HTML Table of Factors
The HTML table below displays the factors of 320 in pairs, making it easier to visualize and understand the factorization process.
| Factor 1 | Factor 2 |
|---|---|
| 1 | 320 |
| 2 | 160 |
| 4 | 80 |
| 5 | 64 |
| 8 | 40 |
| 10 | 32 |
| 16 | 20 |
Examples of Using Factors of 320

The factors of 320, which are 1, 2, 4, 5, 8, 10, 16, 20, 32, 40, 64, 80, 160, and 320, can be utilized in various mathematical operations and practical applications.
Using Factors for Calculations
The factors of 320 can be used to simplify calculations involving this number. For instance, to find half of 320, we can use the factor 2, giving us 160. Similarly, to find a quarter of 320, we can use the factor 4, resulting in 80.
Using Factors for Multiplication and Division
The factors of 320 can be used to perform multiplication and division operations. For example, to multiply 320 by 5, we can use the factor 10, resulting in 3200. To divide 320 by 8, we can use the factor 4, giving us 40.
Using Factors for Solving Equations
The factors of 320 can be used to solve equations involving this number. For instance, to solve the equation x– 8 = 320, we can use the factor 40, resulting in x= 8.
Advanced Applications of Factors of 320

The factors of 320, including 1, 2, 4, 5, 8, 10, 16, 20, 32, 40, 64, 80, 160, and 320, play significant roles in various advanced mathematical concepts. These factors contribute to solving complex mathematical problems in areas such as number theory, algebra, and geometry.
Number Theory
In number theory, the factors of 320 are relevant in understanding the concept of prime factorization. Prime factorization involves expressing a number as a product of its prime factors, which are numbers that can only be divided by themselves and 1. The prime factorization of 320 is 2^65. This factorization helps in determining the properties and relationships of 320 with other numbers.
Essential FAQs
What are the factors of 320?
The factors of 320 are 1, 2, 4, 5, 8, 10, 16, 20, 32, 40, 64, 80, 160, and 320.
How do you find the factors of 320?
To find the factors of 320, we can use prime factorization. 320 = 2^6 – 5. Therefore, the factors of 320 are 1, 2, 4, 5, 8, 10, 16, 20, 32, 40, 64, 80, 160, and 320.
What are the prime factors of 320?
The prime factors of 320 are 2 and 5.